«- back to print version table of contents
Pulse and Multicell Storms Conceptual Model
Definition of Pulse and Multicell Storms
Small multicell storms consist of a number of individual cells in close proximity to each other. These individual cells might share a common precipitation volume, cloud material or a common cold pool. New cells usually initiate before older cells dissipate which means that multicells tend to live considerably longer than any individual updraft.
The focus here is on meso-γ scale (2-20 km; Orlanski 1975) thunderstorms in a low shear environment, or in plainer words, "storm-scale" thunderstorms as opposed to mesoscale convective systems (MCSs). Understanding the environmental deep-layer shear and the system's cold pool strength, two of the more influential drivers of thunderstorm development, provides insight on these storms' appearance and behaviour. In this section we only consider "low shear" environments, subjectively set to 0-25 kts of 0-6 km bulk shear. "High shear" regimes of with 25+ kts of 0-6 km shear are more adequately described in the Supercell and MCS conceptual models.
An organised small multicell is characterised by frequent initiation of new cells which are stronger than their unorganised counterparts. Organising updrafts trend from short-lived pulses to increasingly longer-lived plume-like updrafts that ultimately trend towards supercell characteristics as the ambient deep layer shear and instability is increased.
Among the factors that determine the appearance and behaviour of small multicells are:
- cold pool,
- vertical shear,
- forcing (physical process associated with initation of new deep updrafts),
- ambient instability,
- storm-relative winds,
- and other factors.
For small multicells in weak deep layer shear, the cold pool strength is one of the more influential drivers.
Weak Cold Pool Storm-Scale Multicells
In the weak cold pool scenario (fig. 1), the initiation of new cells is controlled by an external forcing mechanism such as cold fronts, gravity waves or differential heating. New cells tend to form along the axis of forcing, outside the relatively small system cold pool. Depending on the arrangement of the forcing relative to the system, cold pool deficient multicells can propagate backwards (in this case to the left), despite individual cells moving in the opposite direction with the steering flow (in this case to the right). The partial cancellation of propagation and cell motion can lead to a very slow-moving system, enhancing the risk of flash flooding. The weak cold pool multicell shape and movement matches that of the external forcing.

Fig. 1: Top down (A) and side-on (B) views of a conceptual multicell with a weak cold pool which is highlighted in a light blue shading. Cloud is shown in grey shading, approximate 20, 40, 50 dBZ radar reflectivity values are outlined in green, tan, and red dotted lines, respectively. Low level inflow (outflow) is shown in red (blue) streamlines. The double arrow in (A) shows the axis of the vertical cross section shown in (B). In (B), red arrows show updrafts, blue arrows show downdrafts.
Strong Cold Pool Storm-Scale Multicells
In the case of small multicells with a strong cold pool (fig. 2), the initiation of new cells is controlled by the system's cold pool itself. New cell initiation is primarily forced along the leading edge of the cold pool (gust front), and is modulated by environmental factors such as wind shear or instability. The gust front tends to move faster than the individual cells in a low shear setup so that cells initiate, mature as they fall behind the gust front and dissipate as elevated cells on top of the system cold pool. The continual new cell initiation along the fast moving gust front leads to a forward propagating system.

Fig. 1: Conceptual model of a small multicell with a strong cold pool (shaded in blue). Cloud is shown in grey shading, approximate 20, 40, 50 dBZ radar reflectivity values are outlined in green, tan, and red dotted lines, respectively. Low level inflow (outflow) is shown in red (blue) streamlines. The double arrow in (A) shows the axis of the vertical cross section shown in (B). In (B), red arrows show updrafts, blue arrows show downdrafts.
Transition from Weak- to Strong Cold Pool Storm-Scale Multicells
Most small multicells tend to form a deepening and expanding cold pool if they persist or grow upscale. In such an event the system is more likely to initiate new cells along its gust front and become cold pool dominant. This type of transition may also be associated with a distinct change in system movement as cold pool driven propagation is now altering the previous system motion vector.
Pulse and Multicell Storm Structure on Radar
Storm-scale multicell thunderstorms may often look like the ones in the example below. In this case, each individual reflectivity core lasted for only one to two volume scans. The range rings are spaced at 25 km, showing that these clusters of rather intense reflectivity cores do indeed occur on the meso-γ scale. Some of these particular cells are pulse severe storms.

Radar reflectivity image of storm-scale multicell thunderstorms.
Environment and Propogation of Pulse and Multicell Storms
Frequently, multicells don't move simply with the steering flow (i.e., the mass-weighted mean wind in the cloud-bearing layer). Their motion vector possesses a propagation component that is controlled by new cell initiation on a preferred flank; this is particularly true for more organised multicells. Figure 1 shows four of the more influential physical mechanisms that set up such a preferred flank with regard to an existing cold pool.
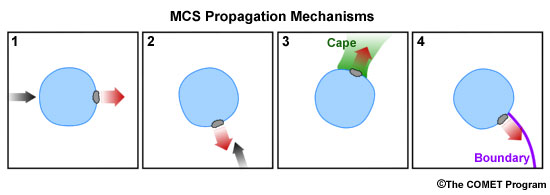
Fig. 1: Conceptual depiction of four of the more prominent physical processes that create a preferred flank for the initiation of new updrafts along a multicell's cold pool boundary. Such directionally selective cell initiation then controls the system's propagation component of the overall motion vector (remember: motion = steering + propagation).
The four mechanisms shown are:
1: Downshear Propagation
2: Propagation Due to Low-level Convergence
3: Propagation into an Axis of Surface-based Instability
4: Propagation Due to Boundary Interactions
At times, more than one of the propagation mechanisms may simultaneously affect a single multicell, which can even lead to splitting of the original system.
Base Propagation Case: No Low-level Shear
Based on idealised numerical simulations, Rotunno et al. (1988) found in the case of zero low-level shear that the relatively warm air outside a cold pool boundary would only be lifted to the top of and then across the cold pool. If the cold pool depth exceeds the local level of free convection (fig. 2: LFC 1, so D>LFC1), initiation would ensue at a random location along the cold pool boundary. If the local LFC is located well above the cold pool depth (LFC 2, with D<LFC 2) the lifting would remain too shallow for initiation.
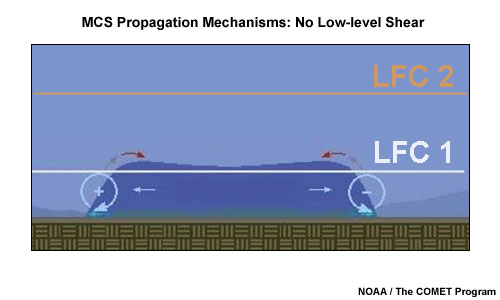
Fig. 2: Conceptual model identifying no preferred flank for new cell initiation along the cold pool edge of an existing multicell in a no shear scenario as outlined in Rotunno et al. (1988).
Propagation Mechanism 1: Downshear Propagation
In the case of nonzero low-level shear over the cold pool depth (say, 3 km) the circulations associated with the cold pool as well as the shear profile interact constructively to generate the deepest lifting of surface parcels on the downshear side of the cold pool. If the lifting is deep enough to reach the local LFC (fig. 3: LFC 2; fig. 2: LFC 1) new initiation is possible.

Fig. 3: Conceptual model identifying the preferred flank for new cell initiation along the cold pool edge of an existing multicell in an environment containing low-level shear as outlined in Rotunno et al. (1988).
An assumption here is that both circulations are of approximately similar magnitudes (cold pool-shear balance). When applying this concept, two issues to consider are the fragility of maintaining the circulation balance between the cold pool and the low-level shear, and the potential influence of other lifting mechanisms outlined below.
Propagation Mechanism 2: Propagation Due to Low-level Convergence
The location where a strong low-level jet impinges upon the cold pool boundary is likely to exhibit strong low-level convergence and parcel lifting over the cold pool. Such lift makes this location a preferred flank for initiation and should therefore lead to a system propagation component (-J) into the low-level jet.
Corfidi et al. (1996; 2003) attempt to quantify the overall system motion for MCSs (fig. 4 A) subject to the described type of propagation process. To match observed multicell motion vectors (V), the studies make a distinction between upwind and downwind-propagating systems. For upwind-propagating multicells, the total motion vector V is the vector sum of the steering flow S and the negative of the low-level storm-relative flow –J. For downwind-propagating multicells (fig. 4 B), we can approximate V as the sum of twice the steering flow and the negative of the low-level storm-relative flow.
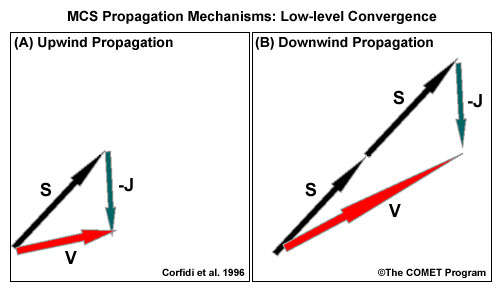
Fig. 4: Estimated total motion vector V for upwind-propagating (A) and downwind-propagating (B) MCSs based on Corfidi et al. (1996). S marks the steering flow (mass-weighted mean wind in the cloud-bearing layer), and -J marks the negative of the maximum low-level storm-relative flow.
The forecast/nowcast application of the total multicell motion vector V estimate should help in the appraisal of the flash flood risk for back-building systems (more likely in case A, upwind propagation) or the risk of damaging winds for forward-propagating systems where steering and propagation vectors are additive (more likely in case B, downwind propagation). Generally, even initially backward propagating systems eventually mature into forward-propagating ones as their cold pool strengthens.
Propagation Mechanism 3: Propagation into an Axis of Surface-based Instability
In a modelling study, Richardson (1999) found that an axis of high surface dewpoints (equating to lower LFCs) intercepting a cold pool boundary leads to a preferred flank for new cell initiation as shallower lifting depth is sufficient here to initiate new cells. This preference can lead to the multicell propagating into the instability axis.
Propagation Mechanism 4: Propagation Due to Boundary Interactions
The intersection points of boundaries, such as a multicell cold pool boundary and some external convergence lines, are preferred points for new initiation (Purdom 1976; Wilson and Schreiber 1986; Fankhauser et al. 1995; Hane et al. 1997; Koch and Ray 1997; Mahoney 1988). Such new "triple point" convection would likely produce a cold pool that merges with the cold pool of the original multicell and could lead to the original multicell being "anchored" to the triple point so that it follows that point's motion instead of moving with the steering flow (Weaver 1979).
Hazards associated with Pulse and Multicell Storms
Severe convective hazards produced by storm-scale multicells are less likely to occur than with their supercell counterparts. Given that the deep layer shear is low, the amount of CAPE available to individual updrafts becomes one of the primary predictors for the likelihood and strength of convective hazards. Individual updrafts have relatively short lifetimes which, probabilistically, puts limits on hail growth potential as well as the production of other convective hazards. In particular, the threat of supercell tornadoes in low shear environments is nearly nonexistent.
Damaging Winds
Especially in a strong CAPE environment containing dry layers of ambient air, stronger pulse updrafts can transport a sufficient amount of moisture to higher levels so that, through evaporation into ambient dry air, a cold dense downdraft can lead to damaging winds on the surface. Alternatively, damaging winds are also more likely with multicells that move embedded in uniformly strong but weakly sheared flow by transporting elevated higher-momentum air to the surface in isolated downdrafts. The likelihood and areal extent of damaging winds also increases as multicells grow upscale and develop stronger, larger cold pools.
Large Hail
Hail can grow to large sizes if hail embryos are exposed to supercooled water, especially in the -10°C to -30°C layer, and if the residence time in such a layer is sufficient. In weak shear and high CAPE environments, updrafts can briefly become quite strong and supply the hail growth layer with plenty of supercooled liquid water, but the pulse nature of those updrafts limits the hail residence time, and therefore the hail size. In a probabilistic sense, it is quite unusual to encounter any hail larger than golf balls with pulse severe storms.
Flash Flooding
The rainfall amount received at a point location is driven by the rain rate and the exposure time to that rain rate. While low-shear multicells (pulse storms) can produce bursts of very intense rain, especially in high CAPE environments, the lack of updraft longevity and size limits the flash flood potential. High CAPE environments with weak steering flow (slow moving cells) or ongoing updraft redevelopment over the same locations provides the optimal setup for flash flood generation. More details can be found in Doswell et al. (1996).
Tornadoes
Supercell tornadoes are very unlikely to occur with multicells embedded in weak deep-layer shear. Non-supercell tornadoes, however, are possible in association with weak shear storm-scale multicells. In the early stages of a growing updraft, vertical vorticity embedded in a boundary below can be vertically stretched to create a ground circulation of tornadic strength if the updraft is growing very vigorously and resides over the boundary for some period of time. This requires very steep lapse rates and weak boundary-relative deep layer flow.
References/Addendum
Corfidi, S.F., J.H. Merritt, and J.M. Fritsch, 1996: Predicting the movement of mesoscale convective complexes. Wea. Forecasting, 11: 41-46.
Corfidi, S. F. 2003: Cold Pools and MCS Propagation: Forecasting the Motion of Downwind-Developing MCSs. Wea. Forecasting, 6: 997–1017.
Doswell, C. A. , H. E. Brooks, R. A. Maddox, 1996: Flash Flood Forecasting: An Ingredients-Based Methodology. Weather and Forecasting, 11: 560-581.
Hane, C. E., H. B. Bluestein, T. M. Crawford, Michael E. Baldwin, Robert M. Rabin, 1997: Severe thunderstorm development in relation to alongdryline variability: A case study. Mon. Wea. Rev., 125: 231–251.
Koch, S, and C. A. Ray, 1997: Mesoanalysis of summertime convergence zones in central and eastern North Carolina. Wea. Forecasting, 12: 56–77.
Mahoney, W.P. III, 1988: Gust front characteristics and the kinematics associated with interacting thunderstorm outflows. Mon. Wea. Rev., 116: 1474-1491.
Purdom, J. F. W., 1976: Some uses of high resolution GOES imagery in the mesoscale forecasting of convection and its behavior. Mon. Wea. Rev., 104: 1474–1483.
Orlanski, I., 1975: A rational subdivision of scales for atmospheric processes. Bulletin of the American Meteorological Society, 56(5): 527-530.
Richardson, Y.P., 1999: The Influence of horizontal variations in vertical shear and low-level moisture on numerically simulated convective storms. Ph.D. Dissertation, School of Meteorology, University of Oklahoma - Norman, 236 pp.
Rotunno, R., J. B. Klemp, M. L. Weisman, 1988: A Theory for Strong, Long-Lived Squall Lines
Journal of the Atmospheric Sciences, 45(3): 463-485.
Weaver, J. F., 1979: Storm Motion as Related to Boundary-Layer Convergence. Mon. Wea. Rev., 107: 612–619.
Wilson, J. W. and W. E. Schreiber, 1986: Initiation of convective storms by radarobserved
boundary layer convergent lines. Mon. Wea. Rev., 114: 2516––2536.