MCS Environment and Propogation
Although MCSs usually develop into a linear mode with a trailing stratiform (TS) region, parallel stratiform (PS) region MCSs or leading stratiform (LS) region MCSs also commonly occur, as outlined below by Parker and Johnson (2000).
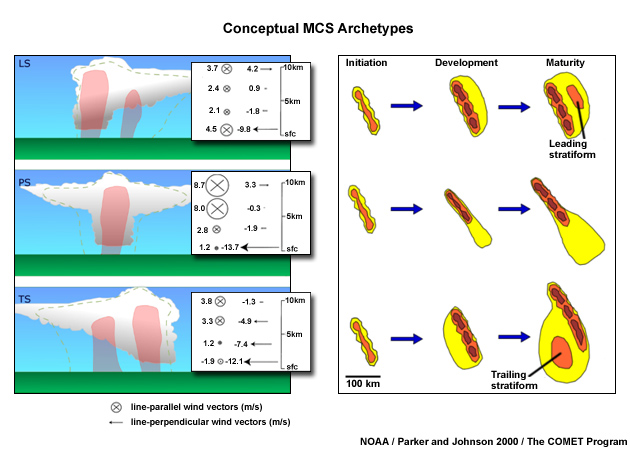
A schematic of three MCS archetypes described in Parker and Johnson (2000). The left side shows vertical profiles of layer-mean storm-relative pre-MCS winds for linear MCS classes. Wind vectors are depicted as line-parallel (X) and line-perpendicular (→) components in m/s. Layers depicted are 0–1, 2–4, 5–8, and 9–10 km The right side of the figure shows the idealised radar reflectivity patterns for each of the three MCS types. Note that the mature reflectivity pattern for the thunderstorm type is specific to the southern hemisphere where the influence of the Coriolis force leads to an enhancement of the trailing stratiform precipitation region on the sourthern end of the convective line.
Table 1 briefly outlines the main attributes of the three MCS types, the formation of which is mainly driven by the system-relative flow at various levels:
| Environmental and Storm Characteristics of MCS Archetypes | |||
|---|---|---|---|
| Leading Stratiform (LS) |
Parallel Stratiform (PS) | Trailing Tratiform (TS) | |
| Upper-level system-relative flow | Rear-to-front | Strongly line-parallel | Front-to-rear |
| Lower-level system-relative flow | Front-to-rear and parallel | Strongly front-to-rear | Strongly front to rear |
| Cold Pool Strength | Weak | Moderate | Strong |
| CAPE (J/kg) | 1009 | 813 | 1605 |
| Propagation Speed (m/s) | 7.1 | 11.4 | 13.0 |
| Mean Duration (h) | 6.5 | 6.3 | 12.2 |
| Occurrence (% of all MCSs) | 20% | 20% | 60% |
Table 1: Outline of various attributes of linear MCSs. Adapted from Parker and Johnson (2000).
MCS Propagation
Frequently, multicells don't move simply with the steering flow (i.e., the mass-weighted mean wind in the cloud-bearing layer). Their motion vector possesses a propagation component that is controlled by new cell initiation on a preferred flank; this is particularly true for more organised multicells. Figure 1 shows four of the more influential physical mechanisms that set up such a preferred flank with regard to an existing cold pool.
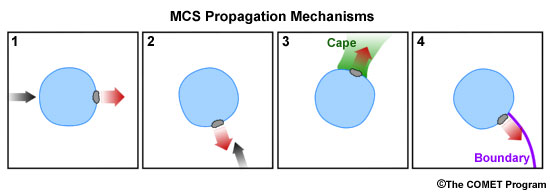
Fig. 1: Conceptual depiction of four of the more prominent physical processes that create a preferred flank for the initiation of new updrafts along a multicell's cold pool boundary. Such directionally selective cell initiation then controls the system's propagation component of the overall motion vector (remember: motion = steering + propagation).
The four mechanisms shown are:
1: Downshear Propagation
2: Propagation Due to Low-level Convergence
3: Propagation into an Axis of Surface-based Instability
4: Propagation Due to Boundary Interactions
At times, more than one of the propagation mechanisms may simultaneously affect a single multicell, which can even lead to splitting of the original system.
Base Propagation Case: No Low-level Shear
Based on idealised numerical simulations, Rotunno et al. (1988) found in the case of zero low-level shear that the relatively warm air outside a cold pool boundary would only be lifted to the top of and then across the cold pool. If the cold pool depth exceeds the local level of free convection (fig. 2: LFC 1, so D>LFC1), initiation would ensue at a random location along the cold pool boundary. If the local LFC is located well above the cold pool depth (LFC 2, with D<LFC 2) the lifting would remain too shallow for initiation.
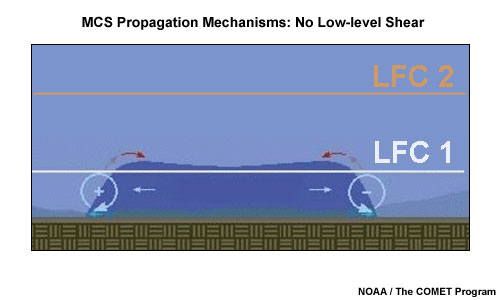
Fig. 2: Conceptual model identifying no preferred flank for new cell initiation along the cold pool edge of an existing multicell in a no shear scenario as outlined in Rotunno et al. (1988).
Propagation Mechanism 1: Downshear Propagation
In the case of nonzero low-level shear over the cold pool depth (say, 3 km) the circulations associated with the cold pool as well as the shear profile interact constructively to generate the deepest lifting of surface parcels on the downshear side of the cold pool. If the lifting is deep enough to reach the local LFC (fig. 3: LFC 2; fig. 2: LFC 1) new initiation is possible.
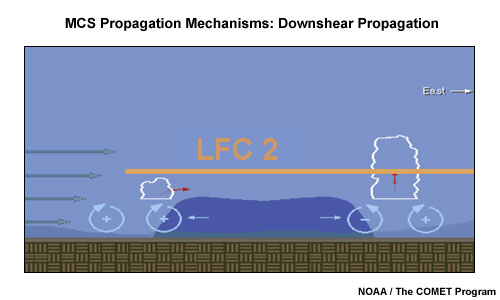
Fig. 3: Conceptual model identifying the preferred flank for new cell initiation along the cold pool edge of an existing multicell in an environment containing low-level shear as outlined in Rotunno et al. (1988).
An assumption here is that both circulations are of approximately similar magnitudes (cold pool-shear balance). When applying this concept, two issues to consider are the fragility of maintaining the circulation balance between the cold pool and the low-level shear, and the potential influence of other lifting mechanisms outlined below.
Propagation Mechanism 2: Propagation Due to Low-level Convergence
The location where a strong low-level jet impinges upon the cold pool boundary is likely to exhibit strong low-level convergence and parcel lifting over the cold pool. Such lift makes this location a preferred flank for initiation and should therefore lead to a system propagation component (-J) into the low-level jet.
Corfidi et al. (1996; 2003) attempt to quantify the overall system motion for MCSs (fig. 4 A) subject to the described type of propagation process. To match observed multicell motion vectors (V), the studies make a distinction between upwind and downwind-propagating systems. For upwind-propagating multicells, the total motion vector V is the vector sum of the steering flow S and the negative of the low-level storm-relative flow –J. For downwind-propagating multicells (fig. 4 B), we can approximate V as the sum of twice the steering flow and the negative of the low-level storm-relative flow.
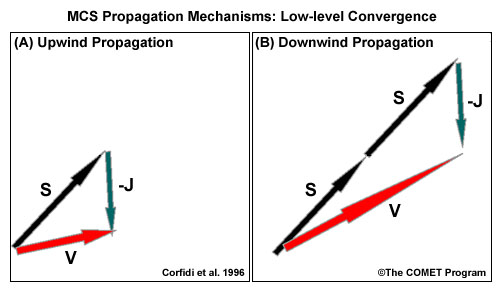
Fig. 4: Estimated total motion vector V for upwind-propagating (A) and downwind-propagating (B) MCSs based on Corfidi et al. (1996). S marks the steering flow (mass-weighted mean wind in the cloud-bearing layer), and -J marks the negative of the maximum low-level storm-relative flow.
The forecast/nowcast application of the total multicell motion vector V estimate should help in the appraisal of the flash flood risk for back-building systems (more likely in case A, upwind propagation) or the risk of damaging winds for forward-propagating systems where steering and propagation vectors are additive (more likely in case B, downwind propagation). Generally, even initially backward propagating systems eventually mature into forward-propagating ones as their cold pool strengthens.
Propagation Mechanism 3: Propagation into an Axis of Surface-based Instability
In a modelling study, Richardson (1999) found that an axis of high surface dewpoints (equating to lower LFCs) intercepting a cold pool boundary leads to a preferred flank for new cell initiation as shallower lifting depth is sufficient here to initiate new cells. This preference can lead to the multicell propagating into the instability axis.
Propagation Mechanism 4: Propagation Due to Boundary Interactions
The intersection points of boundaries, such as a multicell cold pool boundary and some external convergence lines, are preferred points for new initiation (Purdom 1976; Wilson and Schreiber 1986; Fankhauser et al. 1995; Hane et al. 1997; Koch and Ray 1997; Mahoney 1988). Such new "triple point" convection would likely produce a cold pool that merges with the cold pool of the original multicell and could lead to the original multicell being "anchored" to the triple point so that it follows that point's motion instead of moving with the steering flow (Weaver 1979).
