Mesocyclone (mesolow) and Cyclostrophic Flow

The two important radial forces that act on the parcel as it follows a circular path of constant radius $R$ around the center of the mesocyclone (mesolow) are the outward-pointing centrifugal force and the inward-pointing pressure gradient force. The Coriolis effect is small in this scenario, so it is not included in the sum of forces. The mesolow forms as the rotating air parcels are pulled outward from the center by the outward-pointing centrifugal force. In response, the inward pointing pressure gradient force increases until its magnitude is equal to that of the centrifugal force. The outward direction is taken as positive in the polar coordinate system. The radial forces are in balance because the radius of the parcel's path is constant ($r = R$). Therefore, $\frac{1}{\rho}\frac{\Delta P}{\Delta r} = \frac{V^2}{R}$ The equation above is known as the "cyclostrophic equation," and the radial forces on the parcel are said to be in "cyclostrophic balance." The angular speed of the parcel is denoted by $V$. The parcel's angular direction of motion can be either clockwise or counter-clockwise depending on the environmental circumstances that initiates the circular motion.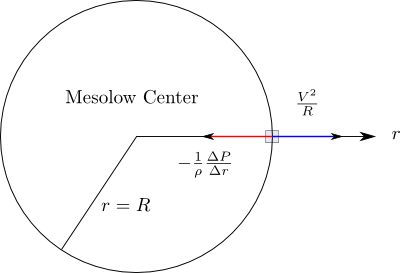

Figure 1. The mesolow and significant radial forces.

Figure 2. Mesolow circulation at different heights.

The development of an enhanced vertical pressure gradient within the mesolow. The dynamics of the mesolow work to enhance the updraft strength and longevity through the development of a vertical pressure gradient. The idealized, three-dimensional mesolow is depicted in Figure 2 with a uniform radius $R$ throughout its depth. The lower level of the cylinder is closer to the surface and the increased friction influence will result in speed $V_1$ being less than $V_2$. The uniform cylinder radius means that $\frac{\Delta P_1}{\Delta R}$ is less than $\frac{\Delta P_2}{\Delta R}$. A greater pressure gradient at level 2 means that the drop in central pressure $P_2$ at level 2 must be greater than the drop in central pressure $P_1$ at level 1. Consequently, the vertical drop in pressure at the center of the low is greater than the "normal" drop at the perimeter of the mesolow cylinder, creating an enhanced updraft at the center of the mesolow.