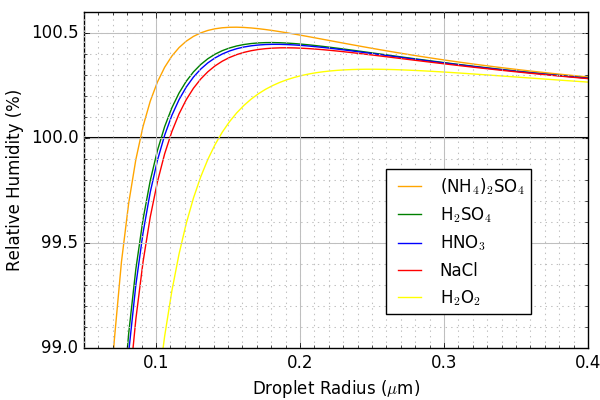
This plot shows the relationship between relative humidity (RH) (the ratio of vapor pressure $e$ required for droplet growth divided by saturation vapor pressure $e_s$) and condensation particle radius for various levels of initial solute. As the radius of the cloud droplet increases, the solute effect decreases, and a higher relative humidity is required for the droplet to grow. This is true for all initial solution concentrations.

The Kohler equation is

$\displaystyle{\frac{e_s^*}{e_s} \approx \frac{exp\left(\frac{c_1}{T\cdot R}\right)}{1+\frac{c_2 \cdot i \cdot m_s}{M_s \cdot R^3}}}$

There are two competing effects represented in the equation. The curvature effect, which inhibits droplet growth (the smaller the diameter, the greater the rate of evaporation from the droplet) is represented in the numerator, and the solute effect (the greater the solution concentration, the smaller the rate of evaporation from the droplet) is represented in the denominator. The solute effect is greater than the curvature effect for smaller radii, because the solute concentration is greater. As the droplet grows in size, the magnitude of both effects decreases (the curvature effect because the radius is increasing, the solute effect because the concentration of the dissolved nuclei decreases as the volume of water increases). However, the solute effect decreases at a greater rate because the volume increases at a rate proportional to $(\Delta R)^3$, while the curvature effect changes at a rate proportional the $\Delta R$. Consequently, the growth of the cloud drop requires a greater relative humidity as the radius increases, eventually reaching a value at which continued growth requires a supersaturated environment.